Ø
The Carnot cycle
is a theoretical thermodynamic cycle proposed by Nicolas Léonard Sadi Carnot in
1824 and expanded by others in the 1830s and 1840s.
Ø
This is most
efficient cycle for converting a thermal energy into work or creating a
temperature different by doing a given amount of work.
Ø
Every
thermodynamics process exits in different state when a system is taken through
these series of different state and then returned its final state a
thermodynamics cycle is said to have occurred.
Ø
In the process of
going through this cycle the system may perform work on its surrounding,
thereby acting as a heat engine.
Ø
Although such a
perfect engine is only a theoretical limit and cannot be built in practices.
1. Reversible isothermal
expansion of the gas at the "hot" temperature, T1
(isothermal heat addition or absorption)
Ø
During this step ( In the Figure A to B ) the gas is allowed to expand and it does work
on the surroundings.
Ø
The temperature
of the gas does not change during the process, thus it is an isothermal expansion.
Ø
The gas expansion
is propelled by absorption of heat energy Q1 and of entropy ΔS = Q1 from the higher
T1
temperature reservoir.
2.Isentropic (reversible
adiabatic) expansion of the gas (isentropic work output).
Ø
For this step ( In the Figure B to C ) the
mechanisms of the engine are assumed to be thermally insulated, thus they
neither gain nor lose heat.
Ø
The gas continues
to expand, doing work on the surroundings, and losing an equivalent amount of
internal energy.
Ø
The gas expansion
causes it to cool to the "cold" temperature, T2. The entropy remains
unchanged.
3.Reversible isothermal compression of the gas at the "cold"
temperature, T2. (isothermal heat rejection)
Ø
( In Figure
C to D) Now the surroundings do work on the gas, causing an amount of heat
energy Q2 and of entropy ΔS = Q2 to flow
T2
out of the gas
to the low temperature reservoir..
Ø
ΔS = Q1
= Q2 ( Clausius
ineqality )
T1 T2
4.Isentropic compression of
the gas (isentropic work input).
Ø
(In Figure D to A) Once again assumed thermally insulated mechanisms of
the engine.
Ø
During this step,
the surrounding do work on the gas, increasing its internal energy and
compressing it causing the temperature to rise T1.
Ø
The entropy
remain unchanged At this point the gas is in the same state as at the start if
step 1.
Work done is given by W = Q1
– Q2
Efficiency η = W = Q1
– Q2 = T1 – T2
Q1 Q1 T1

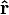 is the unit vector of r
is the unit vector of r
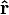 is the unit vector of r
is the unit vector of r


